| Intel and HP illustrate the advantages of EPIC with a
benchmark conceived at Stanford University: the Eight
Queens Problem. The goal is to arrange eight queens on a
chessboard so that no queen threatens any other queen. There are 92 possible solutions. The primary line of C source code that computes the problem translates into machine code that includes three load instructions and three branches. The algorithm would require 13 clock cycles to execute on a traditional CPU. IA-64's speculative loading replaces two of the load instructions (see "Beyond Pentium II," December 1997 BYTE). Predication effectively removes two of the three branches. Together, these techniques reduce the algorithm to seven cycles. However, the most important difference is that predication eliminates the possibility of two mispredicted branches -- potentially saving dozens of cycles, depending on the depth and width of the CPU. Critics claim it's not a good example. "Our customers don't run the Eight Queens Problem very often," says Marc Tremblay, chief CPU architect at Sun Microelectronics. But independent research at universities does indicate that fully predicated instruction sets can eliminate about half of all branches in common code. A Royal Solution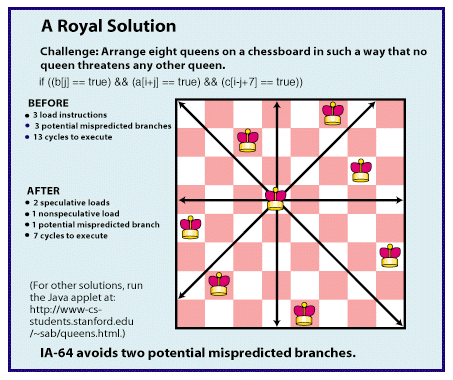 Copyright 1994-1998 BYTE |